What is it and why we want it

The Buy vs. Rent question confuses countless people daily.
We seek help online, being almost invariably mislead by over-simplistic tools.

The plethora of calculators found on the web in the majority of cases do not properly handle several important aspects of the cost/benefit analysis of buying vs. renting.

For instance:

tax-related items, namely the tax benefits of the mortgage interest deduction, also considering the fact that applying it means itemizing deductions, hence losing the standard deduction.
the benefits of re-investing money potentially saved by renting instead of buying,
the benefit of the return of investment of the capital not put into a down-payment.

This calculator (running on shinyapps.io) implements a more comprehensive and realistic picture, including these and other ingredients, and yields a statistical assessment of the buy vs. rent question by means of simulations.

A Simulations-based Approach

Given a set of input parameters, 250 simulations are performed, with stochastic “predictions” of the time varying values of:

property appreciation,
return of investment of the “unused cash” when renting,
inflation,
rent increase (over inflation).

For the first three, values are drawn from Normal distributions with means and standard deviations given among the application inputs. The additional rent increase rate is drawn from an exponential distribution.

For each simulation a ‘trade-off’ value is computed, giving the difference between buying the given property and renting (including the return of the investment of the cash not put into the property) for each year, for the duration of the mortgage loan. Positive values are in favor of buying, negative indicate that renting would be more beneficial financially.

Application Results

The simulations results are summarized in three plots showing:

the trends of the ‘tradeoff’ amount,
the fraction of simulations favoring buying over renting, over time,
the distribution of tradeoff amounts over time, highligthing the distributions at 1/2, 3/4 and at the end of the loan period.

The simulations performed by this simple Application are purely based on general probability density functions, namely Gaussian and Exponential.

However it is clear that for the Annual Variations inputs it would be possible to apply a more real-data-driven approach, by sampling their values from distributions derived from real data from stock market or bonds investment returns, real estate property values, and inflation.

Investment returns could be drawn from a proxy for different investing styles: bond indexes for conservative, S&P500 for middle-ground, NASDAQ composite for more aggressive approach.
Real estate property values could be adjusted regionally, increasing the usefulness and relevance of the Calculator.

The data exist and accessible. I just did not have time to bring them into the fold…

An example is shown below.

Examples of results with their summary plots

Case 1

test_input1 <- list(start_prop_value = 200000, 
                    down_payment_pct = 20.0, 
                    mortgage_rate    = 4.5, 
                    n_years          = 30, 
                    initial_fixed_costs = 6000.0, 
                    prop_tax_rate_pct   =  2.05,
                    prop_insurance      = 4000.0, 
                    HOA_monthly_fee     =  400.0,
                    start_rent          = 1500.0, 
                    rent_insurance      =  260.0, 
                    annual_appreciation    = 3.0, 
                    annual_appreciation_sd = 2.0, 
                    annual_inv             = 5.0, 
                    annual_inv_sd          = 7.0, 
                    annual_inflation       = 1.5, 
                    annual_inflation_sd    = 1.0, 
                    annual_rent_extra_increase_mean = 0.5, 
                    fraction_extra_cash_invested_pct = 50.0, 
                    income_tax_rate_pct = 25.0, 
                    itemized_deductions = 0.0, 
                    std_deduction = 12200, 
                    n_sim = 200)

# tmp.df <- data.frame(value = as.character(unlist(test_input1)))
# row.names(tmp.df) <- names(test_input1)

paramNames <- c("start_prop_value", "down_payment_pct", "mortgage_rate", "n_years", 
                "initial_fixed_costs",
                "prop_tax_rate_pct", "prop_insurance", "HOA_monthly_fee",
                "start_rent", "rent_insurance",
                "annual_appreciation", "annual_appreciation_sd",
                "annual_inv", "annual_inv_sd",
                "annual_inflation", "annual_inflation_sd",
                "annual_rent_extra_increase_mean",
                "fraction_extra_cash_invested_pct",
                "income_tax_rate_pct", "itemized_deductions", "std_deduction",
                "n_sim")

sims.tradeoff1 <- do.call(simulate_tradeoff, getParams1(test_input1, paramNames))
n.sim <- getParams1(test_input1, "n_sim")[[1]]
n.years <- getParams1(test_input1, "n_years")[[1]]

plot_sims(n.sim, n.years, sims.tradeoff1)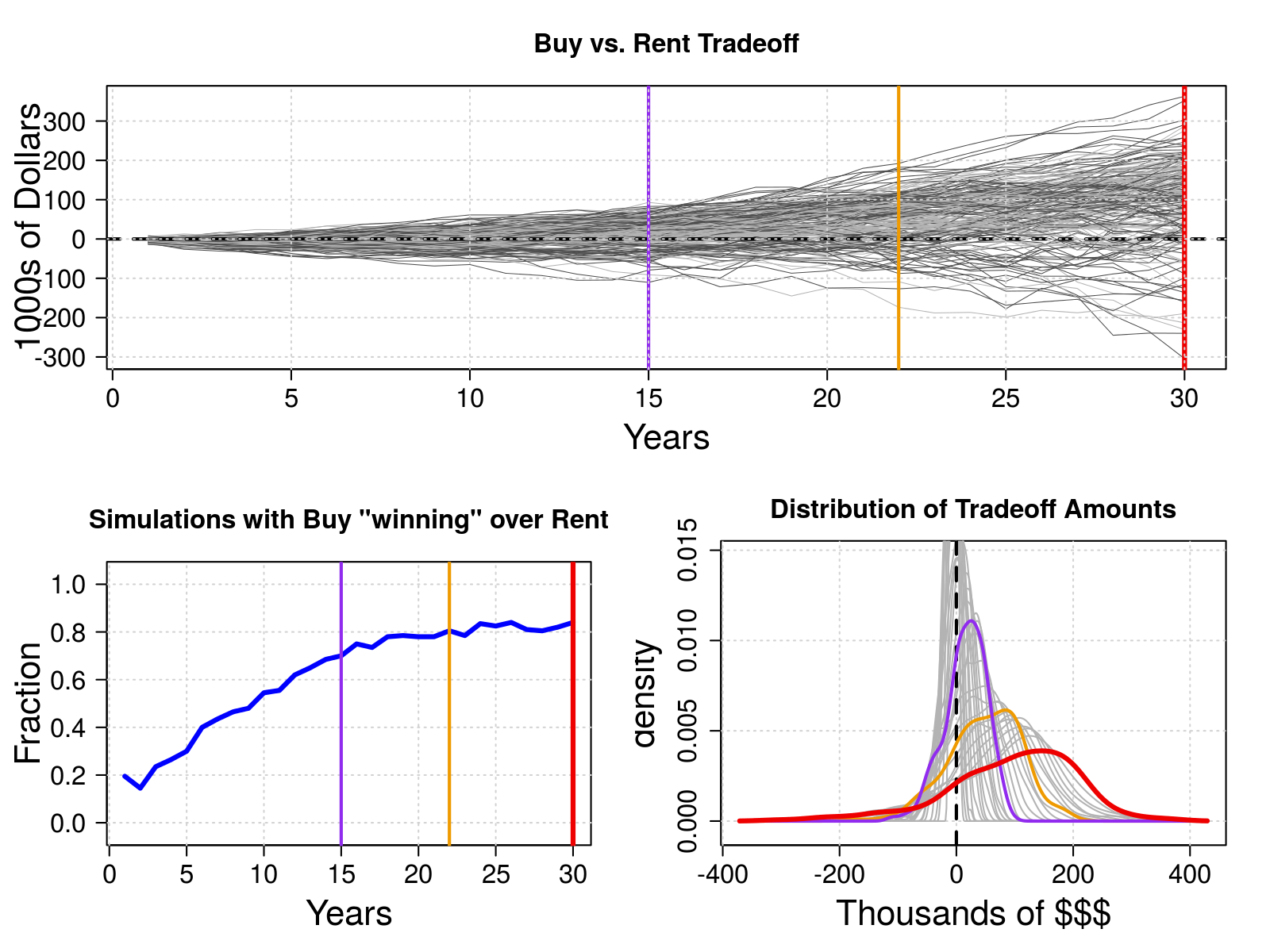

Case 2

The only difference from the previous case is the increase from 6.0% to 6.5% of the mean for the return of investment rate (annual_inv).

test_input2 <- test_input1
test_input2$annual_inv <- 6.5
sims.tradeoff2 <- do.call(simulate_tradeoff, getParams1(test_input2, paramNames))

plot_sims(n.sim, n.years, sims.tradeoff2)

Model Parameters

Buy, Rent and Tax Parameters

Property and mortgage

Purchase price ($)
Down payment (%)
Mortgage interest rate (%)
Duration (years)
Initial fixed costs ($): additional cost incurred when buying a property, e.g. closing costs, or repairs.

Ownership costs: property taxes, insurance, fees

Property tax rate (%)
Insurance cost ($): home-owner insurance premium (annual).
HOA fee ($): home-owner association fees (monthly).

Rent

Rent ($): monthly, ideally for a property comparable to that considered for purchase.
Renter insurance ($)
Fraction of saved cash re-invested (%): if the total costs of renting are lower than those of owning, a portion of the saved cash can be re-invested. This parameter regulates the fraction of this saved cash that is added to the investments.

Annual Variations

Property appreciation

Assuming uncorrelated normally distributed values.

Appreciation (%): mean yearly increase of property values.
Appreciation std. dev. (%): “volatility” of the property value changes.

Cash investment return

Assuming uncorrelated normally distributed values.

Return (%): mean yearly return of cash investments.
Return std. dev. (%): “volatility” of cash investment returns.

Inflation

Assuming uncorrelated normally distributed values.

Inflation (%): mean yearly inflation rate.
Inflation std. dev. (%): “volatility” of inflation.

Rent increase

Extra increase over inflation (%): extra rate of increase of rent, on top of inflation.
Values are drawn from an exponential distribution with this mean.

APPENDIX

Functions

Source code of the user-defined functions:

scripts/my_functions_intro_1.R —

#=-------------------------------------------------------------------------------

cumprod.matrix.old <- function(x) {
    nrows <- dim(x)[1] 
    ncols <- dim(x)[2]
    y <- matrix(1, nrow = nrows, ncol = ncols)
    y[1, ] <- x[1, ]
    for (i in 2:nrows) {
        y[i, ] <- y[i-1, ]*x[i, ]
    }
    return(y)
}

cumprod.matrix <- function(x) {
    nrows <- dim(x)[1] 
    ncols <- dim(x)[2]
    y <- matrix(1, nrow = nrows, ncol = ncols)
    y[1, ] <- x[1, ]
    for (i in 1:ncols) {
        y[, i] <- cumprod(x[, i])
    }
    return(y)
}

cumdiv.matrix <- function(x) {
    nrows <- dim(x)[1] 
    ncols <- dim(x)[2]
    y <- matrix(1, nrow = nrows, ncol = ncols)
    y[1, ] <- x[1, ]
    for (i in 2:nrows) {
        y[i, ] <- x[i, ] / x[i-1, ]
    }
    return(y)
}

cumsum.matrix <- function(x) {
    nrows <- dim(x)[1] 
    ncols <- dim(x)[2]
    y <- matrix(1, nrow = nrows, ncol = ncols)
    y[1, ] <- x[1, ]
    for (i in 1:ncols) {
        y[, i] <- cumsum(x[, i])
    }
    #for (i in 2:nrows) {
    #    y[i, ] <- x[i, ] + x[i-1, ]
    #}
    return(y)
}

cumsub.matrix <- function(x) {
    nrows <- dim(x)[1] 
    ncols <- dim(x)[2]
    y <- matrix(1, nrow = nrows, ncol = ncols)
    y[1, ] <- x[1, ]
    for (i in 2:nrows) {
        y[i, ] <- x[i, ] - x[i-1, ]
    }
    return(y)
}

#=-------------------------------------------------------------------------------

getParams1 <- function(input, pnames) {
    # input[["run_simul"]]

    params <- lapply(pnames, function(p) { input[[p]] })
    names(params) <- pnames
    params
}

#=------------------------------------------------------------------------------

scripts/my_functions_intro_2.R —

#=-------------------------------------------------------------------------------
# setup mortgage quantities

setup_mortgage_monthly <- function(start_prop_value = 300000, 
                                   down_payment_pct = 20.0,
                                   mortgage_rate = 4.5,
                                   n_years = 30) {
    
    #----
    prop.value <- start_prop_value
    down.payment.fraction <- down_payment_pct / 100
    
    rate <- mortgage_rate / 100
    Nm <- 12*n_years
    #----
    
    loan <- prop.value*(1 - down.payment.fraction)
    
    rm <- rate / 12
    rm1 <- 1 + rm
    
    mo.payment <- rm*loan*rm1^Nm/(rm1^Nm - 1)
    
    x1 <- 1:Nm
    x2 <- 2:(Nm+1)
    loan.balance  <- loan*(rm1^Nm - rm1^(x1-1))/(rm1^Nm-1)
    loan.balance2 <- loan*(rm1^Nm - rm1^(x2-1))/(rm1^Nm-1)
    mo.payment.interest <- loan.balance*rm
    mo.payment.principal <- mo.payment - mo.payment.interest
    
    return(data.frame(balance.start = loan.balance, 
                      balance.end = loan.balance2,
                      interest = mo.payment.interest, 
                      principal = mo.payment.principal,
                      mo.payment = rep(mo.payment, Nm),
                      interest.cumul = cumsum(mo.payment.interest),
                      principal.cumul = cumsum(mo.payment.principal),
                      payment.cumul = cumsum(rep(mo.payment, Nm)))
    )
}

#=-------------------------------------------------------------------------------
make_mortgage_annual <- function(monthly_data = NULL) {
    
    annual_data <- monthly_data[ (1:nrow(monthly_data)) %% 12 == 0, c(1, 2, 6, 7, 8)]
    annual_data$balance.start <-  monthly_data$balance.start[ (1:nrow(monthly_data) + 11) %% 12 == 0]
    rownames(annual_data) <- NULL
    annual_data.by_year <- cumsub.matrix(as.matrix(annual_data[, c(3, 4, 5)]))
    df <- data.frame(annual_data, annual_data.by_year)
    colnames(df)[c(6, 7, 8)] <- c("interest.by_year", "principal.by_year", "payment.by_year")
    return(df)
    
}

#=-------------------------------------------------------------------------------
simulate_tradeoff <- function(start_prop_value = NULL,
                              down_payment_pct = NULL,
                              mortgage_rate = NULL,
                              n_years = NULL, 
                              initial_fixed_costs = NULL,
                              prop_tax_rate_pct = NULL,
                              prop_insurance = NULL,
                              HOA_monthly_fee = NULL,
                              start_rent = NULL,
                              rent_insurance = NULL,
                              annual_appreciation = NULL, annual_appreciation_sd = NULL, 
                              annual_inv = NULL, annual_inv_sd = NULL, 
                              annual_inflation = NULL, annual_inflation_sd = NULL, 
                              annual_rent_extra_increase_mean = NULL, 
                              fraction_extra_cash_invested_pct = NULL,
                              income_tax_rate_pct = 25.0,
                              itemized_deductions = 0.0,
                              std_deduction = NULL, 
                              n_sim = 200) {


  #-------------------------------------
  # Setting up mortgage tables
  #-------------------------------------
  mortgage <- setup_mortgage_monthly(start_prop_value = start_prop_value,
                                     down_payment_pct = down_payment_pct,
                                     mortgage_rate = mortgage_rate,
                                     n_years = n_years)

  # mortgage <- do.call(setup_mortgage_monthly, getParams1(input, paramNamesMort)) 
  annual.mortgage <- make_mortgage_annual(monthly_data = mortgage)

  #-------------------------------------
  # Inputs
  #-------------------------------------
  # Initial Property Value
  start.prop_value <- start_prop_value

  # Down Payment
  down.payment <- start.prop_value*down_payment_pct / 100.0

  # Additional Fixed Initial Costs
  initial.fixed_costs <- initial_fixed_costs

  # Initial Property Insurance [index to INFLATION]
  prop.insurance <- prop_insurance

  # Property Tax Rate
  prop.tax.rate <- prop_tax_rate_pct / 100

  # HOA fees [index to INFLATION]
  HOA.monthly.fee <- HOA_monthly_fee
  HOA.annual.fee <- HOA.monthly.fee * 12.0

  # Initial Monthly Rent [index to ~INFLATION]
  start.rent = start_rent

  # Monthly Rent Increase (use `rexp` to draw an increment over inflation rate)
  annual.rent.mean <- annual_rent_extra_increase_mean / 100

  # Initial Renter Insurance [index to INFLATION]
  rent.insurance <- rent_insurance

  # Fraction of extra cash re-invested
  fraction.extra_cash_invested <- fraction_extra_cash_invested_pct / 100

  # Income Tax Rate
  income.tax.rate <- income_tax_rate_pct / 100

  # Std Deduction [index to INFLATION]
  std.deduction <- std_deduction

  # Other Itemized Deductions [index to INFLATION] 
  itemized.deductions <- itemized_deductions

  #-------------------------------------------------
  # Property Appreciation
  annual.appr    <- annual_appreciation / 100
  annual.appr.sd <- annual_appreciation_sd / 100

  # Investment
  annual.invest    <- annual_inv / 100
  annual.invest.sd <- annual_inv_sd / 100

  # Inflation
  annual.inflation    <- annual_inflation / 100
  annual.inflation.sd <- annual_inflation_sd / 100
  #-------------------------------------------------

  # Number of observations (in Years)
  n.years <- n_years
  # number of months to simulate
  n.periods <- 1
  n.obs <- n.periods * n.years

  # Number of simulations
  n.sim <- n_sim

  #-------------------------------------------------
  # Spreading the rate quantities to sub-periods (not necessarily months maybe)
  #-------------------------------------------------
  # Property Appreciation
  monthly.appr    <- annual.appr / n.periods
  monthly.appr.sd <- annual.appr.sd / sqrt(n.periods)

  # Investment
  monthly.invest    <- annual.invest / n.periods
  monthly.invest.sd <- annual.invest.sd / sqrt(n.periods)

  # Inflation
  monthly.inflation    <- annual.inflation / n.periods
  monthly.inflation.sd <- annual.inflation.sd / sqrt(n.periods)

  #----
  # The following should be updated only at the full years
  # extra rent increase
  # monthly.rent.lambda <- annual.rent.mean / n.periods
  annual.rent.lambda <- 1.0 / annual.rent.mean


  #-------------------------------------------------
  # simulate Returns
  monthly.appr.returns      <- matrix(0, n.obs, n.sim)
  monthly.invest.returns    <- matrix(0, n.obs, n.sim)
  monthly.inflation.returns <- matrix(0, n.obs, n.sim)
  # monthly.rent.returns      <- matrix(0, n.obs, n.sim)       # rent should really be increase only yearly

  monthly.appr.returns[]      <- rnorm(n.obs*n.sim, mean = monthly.appr, sd = monthly.appr.sd)
  monthly.invest.returns[]    <- rnorm(n.obs*n.sim, mean = monthly.invest, sd = monthly.invest.sd)
  monthly.inflation.returns[] <- rnorm(n.obs*n.sim, mean = monthly.inflation, sd = monthly.inflation.sd)
  # Not allowing for deflation
  monthly.inflation.returns   <- ifelse(monthly.inflation.returns <= 0, 0.0, monthly.inflation.returns)

  # resets first-year inflation rate to zero.
  monthly.inflation.returns[1:n.periods, ] <- 0.0

  annual.appr.returns.cumul <- cumprod.matrix(1 + monthly.appr.returns)[ (1:n.obs) %% n.periods == 0, ]
  annual.appr.returns       <- cumdiv.matrix(annual.appr.returns.cumul) - 1.0
  annual.appr.returns[1, ]  <- 0.0 

  annual.invest.returns.cumul <- cumprod.matrix(1 + monthly.invest.returns)[ (1:n.obs) %% n.periods == 0, ]
  annual.invest.returns       <- cumdiv.matrix(annual.invest.returns.cumul) - 1.0
  annual.invest.returns[1, ]  <- 0.0 

  annual.inflation.returns.cumul <- cumprod.matrix(1 + monthly.inflation.returns)[ (1:n.obs) %% n.periods == 0, ]
  annual.inflation.returns       <- cumdiv.matrix(annual.inflation.returns.cumul) - 1.0
  annual.inflation.returns.cumul[1, ]  <- 1.0 
  annual.inflation.returns[1, ]  <- 0.0 

  # FUDGE to set a constant rent increase
  if( annual.inflation.sd == 0 ) {
    annual.rent.increases      <- 0.0*annual.inflation.returns + annual.rent.mean
    annual.rent.increases[1, ] <- 0.0 
  } else {
  # REAL
    annual.rent.increases      <- annual.inflation.returns + rexp(n.years*n.sim, rate = annual.rent.lambda)
  }

  #-------------------------------------------------
  sim.prop_value      <- matrix(start.prop_value, n.years, n.sim) * annual.appr.returns.cumul

  sim.prop.insurance <- matrix(prop.insurance, n.years, n.sim) * annual.inflation.returns.cumul
  sim.HOA.fee        <- matrix(HOA.annual.fee, n.years, n.sim) * annual.inflation.returns.cumul

  sim.rent           <- 12*start.rent*cumprod.matrix(1 + annual.rent.increases)

  sim.mort.interest  <- matrix(annual.mortgage$interest.by_year, n.years, n_sim)

  # Costs
  sim.own.costs <- sim.prop_value*prop.tax.rate + sim.prop.insurance + sim.HOA.fee
  sim.own.costs[1, ] <- sim.own.costs[1, ] + initial.fixed_costs

  sim.own.costs.with.mortgage <- sim.own.costs + annual.mortgage$payment.by_year

  # Tax Savings (or not)
  sim.deductions <- sim.mort.interest + sim.prop_value*prop.tax.rate + itemized.deductions*annual.inflation.returns.cumul
  sim.tax.savings <- ifelse(sim.deductions > std.deduction*annual.inflation.returns.cumul, 
                            income.tax.rate*(sim.deductions-std.deduction*annual.inflation.returns.cumul),
                            0)

  # True Cost (= Costs - Tax Savings)
  sim.own.true.cost <- sim.own.costs + annual.mortgage$payment.by_year - sim.tax.savings

  # Renting Costs
  sim.rent.cost <- sim.rent + rent.insurance*annual.inflation.returns.cumul
  # sim.rent.cost <- sim.rent 

  # Extra Cash and re-investment
  sim.cost.delta <- sim.own.true.cost - sim.rent.cost
  sim.extra.cash <- ifelse(sim.cost.delta > 0, sim.cost.delta, 0)

  sim.invest <- matrix(down.payment, n.years, n.sim) * annual.invest.returns.cumul
  sim.invest.alt <- sim.invest

  for (j in 2:n.obs) {
    sim.invest.alt[j, ] = (sim.invest.alt[j-1, ] + sim.extra.cash[j-1, ]*fraction.extra_cash_invested)*(1+annual.invest.returns[j,]) 
                         + sim.extra.cash[j-1, ]*(1-fraction.extra_cash_invested)
  }

  sim.tradeoff <- -1*cumsum.matrix(sim.cost.delta) + (sim.prop_value - annual.mortgage$balance.end) - sim.invest.alt

  return(sim.tradeoff)
}

#=-------------------------------------------------------------------------------
plot_sims <- function(n.sim, n.years, sim.to) {
    
    par(cex.main = 1.5)
    par(cex.lab = 2.0)
    par(cex.axis = 1.5)

    # layout3 : 1 / 2 
    shape1 <- c(rep(1,8))
    shape2 <- c(rep(2,4), rep(3,4))
    shape <- c( rep(shape1, 5), rep(shape2, 5))
    mat.layout3 <- matrix(shape, nrow = 10, ncol = 8, byrow = TRUE)
    layout(mat.layout3)
    
    palette(c("black", "grey50", "grey30", "grey70", "orange", "#0f23d9"))
    palette(rep(c("grey30", "grey70"), 3))

    ny1 <- floor(n.years*3/4)
    ny2 <- floor(n.years/2)
    
    #--------------------------------------------------
    # time-series
    par(mar =  c(5, 5, 4, 2) + 0.1)
    matplot(sim.to/1000, type="l", lwd=0.5, lty=1, col=1:6, 
        las = 1, 
            xlab = 'Years', 
        ylab = '1000s of Dollars', 
            main = 'Buy vs. Rent Tradeoff')
    abline(h=0, col="black", lty=2, lwd=2)
    abline(v=ny1, col="orange2", lwd=2)
    abline(v=ny2, col="purple2", lwd=2)
    abline(v=n.years, col="red2", lwd=3)
    grid()
    
    #--------------------------------------------------
    # positive fraction 
    fraction.positive <- rowSums(sim.to > 0)/n.sim
    plot(1:length(fraction.positive), fraction.positive, type="n", 
         ylim = c(-0.05, 1.05),
     las = 1,
         xlab = 'Years', 
     ylab = 'Fraction', 
         main = 'Simulations with Buy "winning" over Rent')
    grid()
    lines(1:length(fraction.positive), fraction.positive, col="blue", lwd = 3)
    abline(v=ny1, col="orange2", lwd=2)
    abline(v=ny2, col="purple2", lwd=2)
    abline(v=n.years, col="red2", lwd=3)
    
    #--------------------------------------------------
    # density distributions
    # i.years <- (1:n.years)[(1:n.years) %% 5 == 0]
    i.years <- 1:n.years
    # i.years <- 1:nrow(sim.to)
    
    to.range <- range(sim.to[i.years, ])/1000.
    to.xmin <- to.range[1] - 0.1*(to.range[2] - to.range[1])
    to.xmax <- to.range[2] + 0.1*(to.range[2] - to.range[1])
    
    to.distr <- matrix(0, length(i.years), n.sim)
    to.dens.x <- matrix(0, length(i.years), 512)
    to.dens.y <- matrix(0, length(i.years), 512)
    
    for( ii in 1:length(i.years) ) {
        iy <- i.years[ii]
        to.distr[ii, ] <- sim.to[iy, ]/1000.
    }
    
    for( ii in 1:length(i.years) ) {
        to.dens.x[ii, ] <- density(to.distr[ii, ], n=512, from=to.xmin, to=to.xmax)$x
        to.dens.y[ii, ] <- density(to.distr[ii, ], n=512, from=to.xmin, to=to.xmax)$y
    }
    tod.max <- max(to.dens.y[13:n.years, ])
    tod.min <- 0.0 - 0.05*tod.max
    tod.max <- 1.05*tod.max
    
    # to.dens.toplot.x <- density(sim.to[ny, ]/1000, n=512, from=to.xmin, to=to.xmax)$x
    # to.dens.toplot.y <- density(sim.to[ny, ]/1000, n=512, from=to.xmin, to=to.xmax)$y
    to.dens.toplot.x <- density(sim.to[nrow(sim.to), ]/1000, n=512, from=to.xmin, to=to.xmax)$x
    to.dens.toplot.y <- density(sim.to[nrow(sim.to), ]/1000, n=512, from=to.xmin, to=to.xmax)$y
    
    par(mar=c(5,4,3,2)+0.1)
    plot(to.dens.y, type="n", 
         xlim = c(to.xmin, to.xmax), 
     ylim = c(tod.min, tod.max),
     xlab = 'Thousands of $$$',
     ylab = "density",
         main = "Distribution of Tradeoff Amounts")
    grid()

    for( ii in 1:length(i.years) ) {
        lines(to.dens.x[ii, ], to.dens.y[ii, ], col="grey70", lwd=1)
    }
    abline(v=0, col="black", lty = 2, lwd = 2)
    lines(to.dens.x[ny1, ], to.dens.y[ny1, ], col="orange2", lwd=2)
    lines(to.dens.x[ny2, ], to.dens.y[ny2, ], col="purple2", lwd=2)
    lines(to.dens.toplot.x, to.dens.toplot.y, col="red2", lwd=3)

}

#=-------------------------------------------------------------------------------

R Session Info

sessionInfo()
# R version 3.1.3 (2015-03-09)
# Platform: x86_64-pc-linux-gnu (64-bit)
# Running under: Ubuntu 14.04.2 LTS
# 
# locale:
#  [1] LC_CTYPE=en_US.UTF-8       LC_NUMERIC=C               LC_TIME=en_US.UTF-8       
#  [4] LC_COLLATE=C               LC_MONETARY=en_US.UTF-8    LC_MESSAGES=en_US.UTF-8   
#  [7] LC_PAPER=en_US.UTF-8       LC_NAME=C                  LC_ADDRESS=C              
# [10] LC_TELEPHONE=C             LC_MEASUREMENT=en_US.UTF-8 LC_IDENTIFICATION=C       
# 
# attached base packages:
# [1] stats     graphics  grDevices utils     datasets  methods   base     
# 
# other attached packages:
# [1] ggplot2_1.0.1 magrittr_1.5  tidyr_0.2.0   dplyr_0.4.2   knitr_1.10.5 
# 
# loaded via a namespace (and not attached):
#  [1] DBI_0.3.1        MASS_7.3-41      R6_2.0.1         Rcpp_0.11.6      assertthat_0.1  
#  [6] colorspace_1.2-6 digest_0.6.8     evaluate_0.7     formatR_1.2      grid_3.1.3      
# [11] gtable_0.1.2     htmltools_0.2.6  munsell_0.4.2    parallel_3.1.3   plyr_1.8.3      
# [16] proto_0.3-10     reshape2_1.4.1   rmarkdown_0.7    scales_0.2.4     stringi_0.5-5   
# [21] stringr_1.0.0    tools_3.1.3      yaml_2.1.13

Buy vs. Rent App

a simulation-based calculator

Giovanni Fossati

What is it and why we want it

A Simulations-based Approach

Application Results

Examples of results with their summary plots

Case 1

Case 2

Model Parameters

Buy, Rent and Tax Parameters

Property and mortgage

Ownership costs: property taxes, insurance, fees

Rent

Annual Variations

Property appreciation

Cash investment return

Inflation

Rent increase

APPENDIX

Functions

R Session Info

Buy vs. Rent App

a simulation-based calculator

Giovanni Fossati

What is it and why we want it

A Simulations-based Approach

Application Results

Examples of results with their summary plots

Case 1

Case 2

Model Parameters

Buy, Rent and Tax Parameters

Property and mortgage

Ownership costs: property taxes, insurance, fees

Rent

Income Tax Related

Annual Variations

Property appreciation

Cash investment return

Inflation

Rent increase

APPENDIX

Functions

R Session Info